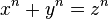“Eu tenho uma demonstração realmente maravilhosa para esta proposição, mas este doodle é muito pequeno para contê-la”, é o que diz o título da imagem na página inicial do Google.
Sobre Pierre de Fermat
Segundo o artigo colaborativo no Wikipédia, as contribuições de Fermat para o cálculo geométrico e infinitesimal foram inestimáveis. Ele obtinha, com seus cálculos, a área de parábolas e hipérboles, determinava o centro de massa de vários corpos, etc. Em 1934, Louis Trenchard Moore descobriu uma nota de Isaac Newton dizendo que seu cálculo, antes tido como de invenção independente, fora baseado no “método de monsieur Fermat para estabelecer tangentes”. Foi a primeira pessoa a enunciar o pequeno teorema de Fermat, embora a primeira pessoa a publicar a prova do teorema foi Euler em 1736 no artigo “Theorematum Quorundam ad Números Primos Spectantium Demonstratio”.
Contudo, o que mais interessava a Fermat, na verdade, era um ramo da Matemática chamado teoria dos números, que tem poucas aplicações práticas claras. É da teoria dos números seu famoso teorema, conhecido como Último Teorema de Fermat.
Este teorema tem um enunciado extremamente simples:
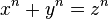
não existe para x, y, z inteiros e positivos e n inteiro, positivo e n> 2.
O teorema foi escrito nas margens do Aritmética de Diofante, seguido de uma frase: “Eu tenho uma demonstração realmente maravilhosa para esta proposição, mas esta margem é muito estreita para contê-la”. Aliás, escrever nas margens dos livros era um costume de Fermat e foi graças ao seu filho mais velho, Clément-Samuel, que suas anotações não se perderam para sempre. Clément-Samuel, depois de passar cinco anos recolhendo cartas e anotações de seu pai, publica em 1670, em Toulouse, a Aritmética de Diofante contendo observações de Pierre de Fermat, cuja página 61 continha o teorema.
Naturalmente, há quem duvide que ele tenha dito a verdade. Gerações inteiras de matemáticos têm amaldiçoado a falta de espaço daquela margem. Por mais de três séculos, praticamente todos os grandes expoentes da Matemática (entre eles Euler e Gauss) debruçaram-se sobre o assunto. Com o advento dos computadores foram testados milhões de algarismos com diferentes valores para x, y, z e n e a igualdade xn + yn = zn não se verificou. Assim empiricamente se comprova que Fermat tenha razão. Mas e a demonstração? Um renomado empresário e matemático alemão – Paul Wolfskehl – na noite que decidira suicidar-se em sua biblioteca, depara com o Último Teorema de Fermat, e muda de idéia. Em seu testamento, deixou em 1906 a quantia de 100.000 marcos para quem o demonstrasse.
O teorema desafiou matemáticos por todo o mundo durante 358 anos, até que Andrew Wiles, um matemático britânico, conseguisse demonstrá-lo, primeiramente em 1993 e, depois de consertar alguns dos erros apontados, definitivamente em 1995. Cumpre esclarecer que Wiles utilizou conceitos avançadíssimos, com os quais Fermat nem poderia ter sonhado. Assim chega ao fim uma história épica na busca do Santo Graal da Matemática.
Fonte:site Bagarai.
RIO - "Você sabe muito mais matemática do que pensa que sabe." A frase de incentivo não é para nenhum aluno de colégio, mas para o pai e a mãe do estudante. Parte da introdução de "Matemática para pais e professores das séries iniciais", de Osmar Nina Garcia Neto e João Batista Araujo e Oliveira, a frase também deu o tom de um seminário ocorrido este mês no Rio, para discutir justamente o ensino de matemática pelos estudantes do nível fundamental. Muito do problema com a matemática, disciplina que tem alguns dos piores índices de aprendizagem - não alcança 20% o percentual de alunos no país que chegam ao fim do fundamental sabendo o adequado para a sua série em matemática, segundo dados do Sistema de Avaliação da Educação Básica (Saeb) -, vem não só de um ensino escolar deficiente ou pouco estimulante, mas também do medo que os próprios pais têm do assunto e o transmitem aos filhos.
